Specifying rotations or origin shifts in Potential classes

Most of the gravitational potential classes implemented in gala support shifting the origin of the potential relative to the coordinate system, and specifying a rotation of the potential relative to the coordinate system. By default, the origin is assumed to be at (0,0,0) or (0,0), and there is no rotation assumed.

For the examples below the following imports have already been executed:

>>> import astropy.units as u
>>> import numpy as np
>>> import gala.potential as gp
>>> from gala.units import galactic, solarsystem

Origin shifts

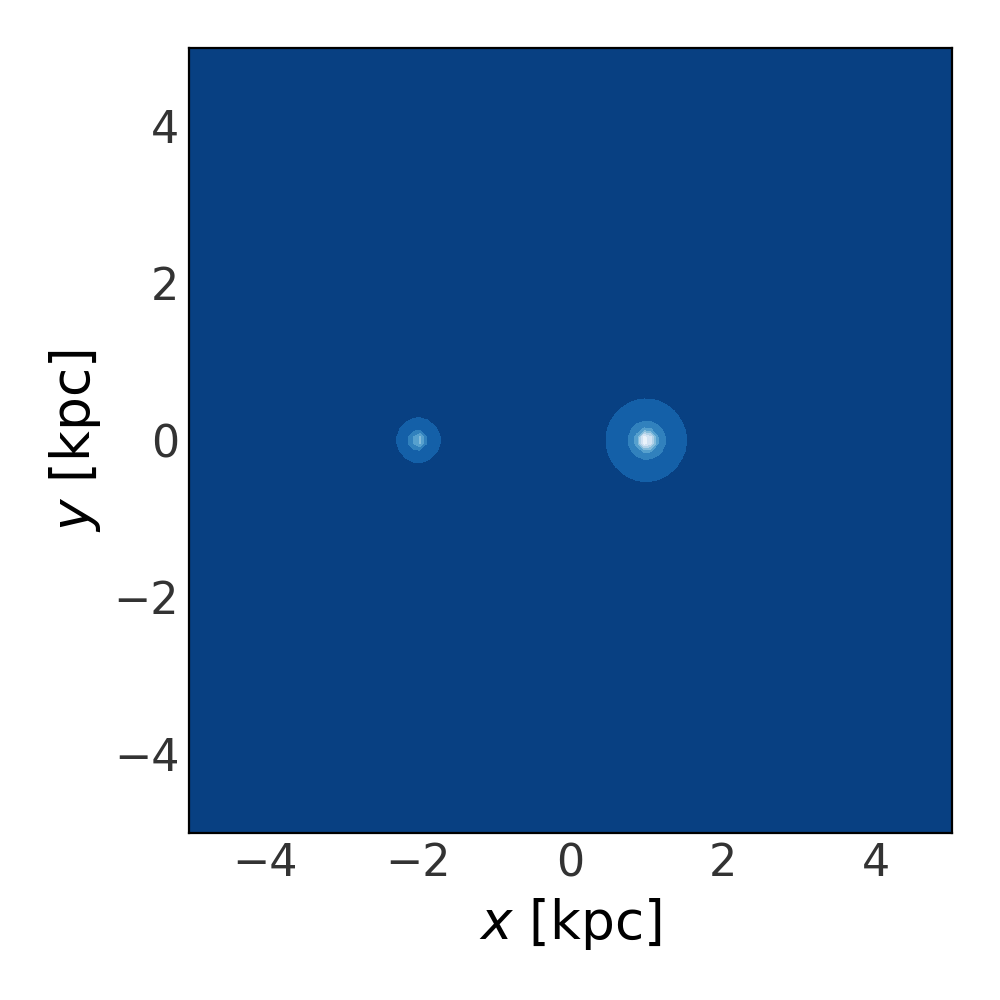
For potential classes that support these options, origin shifts are specified by passing in a Quantity to set the origin of the potential in the given coordinate system. For example, if we are working with two KeplerPotential objects, and we want them to be offset from one another such that one potential is at (1, 0, 0) AU and the other is at (-2, 0, 0) AU, we would define the two objects as:

>>> p1 = gp.KeplerPotential(m=1*u.Msun, origin=[1, 0, 0]*u.au,
...                         units=solarsystem)
>>> p2 = gp.KeplerPotential(m=0.5*u.Msun, origin=[-2, 0, 0]*u.au,
...                         units=solarsystem)

To see that these are shifted from the coordinate system origin, let’s combine these two objects into a CCompositePotential and visualize the potential:

>>> pot = gp.CCompositePotential(p1=p1, p2=p2)
>>> fig, ax = plt.subplots(1, 1, figsize=(5, 5))
>>> grid = np.linspace(-5, 5, 100)
>>> p.plot_contours(grid=(grid, grid, 0.), ax=ax)
>>> ax.set_xlabel("$x$ [kpc]")
>>> ax.set_ylabel("$y$ [kpc]")

(Source code, png, pdf)

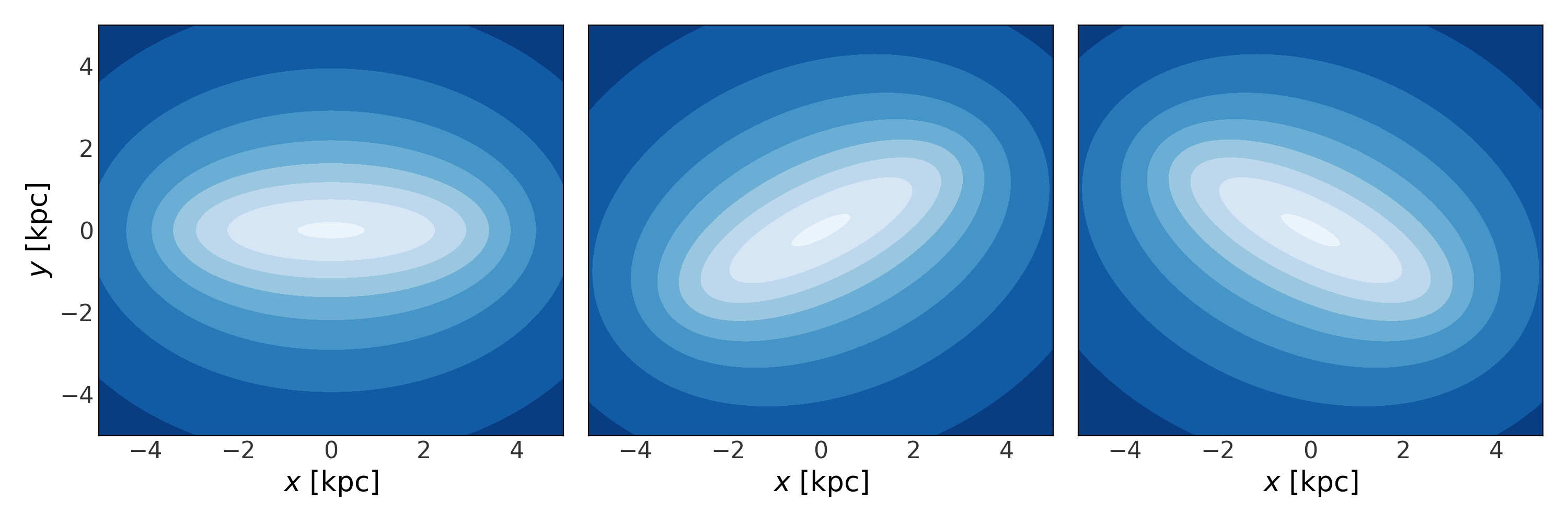
Rotations

Rotations can be specified either by passing in a scipy.spatial.transform.Rotation instance, or by passing in a 2D numpy array specifying a rotation matrix. For example, let’s see what happens if we rotate a bar potential using these two possible inputs. First, we’ll define a rotation matrix specifying a 30 degree rotation around the z axis (i.e. counter-clockwise) using astropy.coordinates.matrix_utilities.rotation_matrix. Next, we’ll define a rotation using a scipy Rotation object:

>>> from astropy.coordinates.matrix_utilities import rotation_matrix
>>> from scipy.spatial.transform import Rotation
>>> R_arr = rotation_matrix(30*u.deg, 'z')
>>> R_scipy = Rotation.from_euler('z', 30, degrees=True)

Warning

Note that astropy and scipy have different rotation conventions, so even though both of the above look like identical 30 degree rotations around the z axis, they result in different (i.e. transposed or inverse) rotation matrices:

>>> R_arr
array([[ 0.8660254,  0.5      ,  0.       ],
       [-0.5      ,  0.8660254,  0.       ],
       [ 0.       ,  0.       ,  1.       ]])
>>> R_scipy.as_matrix()
array([[ 0.8660254, -0.5      ,  0.       ],
       [ 0.5      ,  0.8660254,  0.       ],
       [ 0.       ,  0.       ,  1.       ]])

Let’s see what happens to the bar potential when we specify these rotations:

>>> bar1 = gp.LongMuraliBarPotential(m=1e10, a=3.5, b=0.5, c=0.5,
...                                  units=galactic)
>>> bar2 = gp.LongMuraliBarPotential(m=1e10, a=3.5, b=0.5, c=0.5,
...                                  units=galactic, R=R_arr)
>>> bar3 = gp.LongMuraliBarPotential(m=1e10, a=3.5, b=0.5, c=0.5,
...                                  units=galactic, R=R_scipy)

(Source code, png, pdf)