Gravitational potentials (gala.potential)#
Introduction#
This subpackage provides a number of classes for working with parametric models
of gravitational potentials. There are a number of built-in potentials
implemented in C and Cython (for speed), and there are base classes that allow
for easy creation of new custom potential classes
in pure Python or by writing custom C/Cython extensions. The Potential
objects have convenience methods for computing common dynamical quantities, for
example: potential energy, spatial gradient, density, or mass profiles. These
are particularly useful in combination with the integrate and
dynamics subpackages.
Also defined in this subpackage are a set of reference frames which can be used
for numerical integration of orbits in non-static reference frames. See the page
on Hamiltonian objects and reference frames for more information. Potential
objects can be combined with a reference frame and stored in a
Hamiltonian object that provides an easy interface
to numerical orbit integration.
For the examples below the following imports have already been executed:
>>> import astropy.units as u
>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> import gala.potential as gp
>>> from gala.units import galactic, solarsystem, dimensionless
Getting Started: Built-in Methods of Potential Classes#
Any of the built-in Potential classes are initialized by passing in keyword
argument parameter values as Quantity objects or as
numeric values in a specified unit system. To see what parameters are available
for a given potential, check the documentation for the individual classes below.
You must also specify a UnitSystem when initializing a potential.
A unit system is a set of non-reducible units that define (at minimum) the
length, mass, time, and angle units. A few common unit systems are built in to
the package (e.g., galactic, solarsystem, dimensionless). For
example, to create an object to represent a Kepler potential (point mass) at the
origin with mass = 1 solar mass, we would instantiate a
KeplerPotential object:
>>> ptmass = gp.KeplerPotential(m=1.*u.Msun, units=solarsystem)
>>> ptmass
<KeplerPotential: m=1.00 (AU,yr,solMass,rad)>
If you pass in parameters with different units, they will be converted to the specified unit system:
>>> gp.KeplerPotential(m=1047.6115*u.Mjup, units=solarsystem)
<KeplerPotential: m=1.00 (AU,yr,solMass,rad)>
If no units are specified for a parameter (i.e. a parameter value is passed in
as a Python numeric value or array), it is assumed to be in the specified
UnitSystem:
>>> gp.KeplerPotential(m=1., units=solarsystem)
<KeplerPotential: m=1.00 (AU,yr,solMass,rad)>
The potential classes work well with the astropy.units framework, but to
ignore units you can use the DimensionlessUnitSystem or pass
None as the unit system:
>>> gp.KeplerPotential(m=1., units=None)
<KeplerPotential: m=1.00 (dimensionless)>
All of the built-in potential objects have defined methods to evaluate the
potential energy and the gradient/acceleration at a given position or array of
positions. For example, to evaluate the potential energy at the 3D position
(x, y, z) = (1, -1, 0) AU:
>>> ptmass.energy([1., -1., 0.] * u.au)
<Quantity [-27.91440236] AU2 / yr2>
These functions also accept both Quantity objects or
plain ndarray-like objects (in which case the position is
assumed to be in the unit system of the potential):
>>> ptmass.energy([1., -1., 0.])
<Quantity [-27.91440236] AU2 / yr2>
This also works for multiple positions by passing in a 2D position (but see Conventions for a description of the interpretation of different axes):
>>> pos = np.array([[1., -1. ,0],
... [2., 3., 0]]).T
>>> ptmass.energy(pos * u.au)
<Quantity [-27.91440236, -10.94892941] AU2 / yr2>
We can also compute the gradient or acceleration:
>>> ptmass.gradient([1., -1., 0] * u.au)
<Quantity [[ 13.95720118],
[-13.95720118],
[ 0. ]] AU / yr2>
>>> ptmass.acceleration([1., -1., 0] * u.au)
<Quantity [[-13.95720118],
[ 13.95720118],
[ -0. ]] AU / yr2>
Most of the potential objects also have methods implemented for computing the
corresponding mass density and the Hessian of the potential (the matrix of 2nd
derivatives) at given locations. For example, with the
HernquistPotential, we can evaluate both the
mass density and Hessian at the position (x, y, z) = (1, -1, 0) kpc:
>>> pot = gp.HernquistPotential(m=1E9*u.Msun, c=1.*u.kpc, units=galactic)
>>> pot.density([1., -1., 0] * u.kpc)
<Quantity [7997938.82200887] solMass / kpc3>
>>> pot.hessian([1., -1., 0] * u.kpc)
<Quantity [[[ -4.68318131e-05],
[ 5.92743432e-04],
[ 0.00000000e+00]],
[[ 5.92743432e-04],
[ -4.68318131e-05],
[ 0.00000000e+00]],
[[ 0.00000000e+00],
[ 0.00000000e+00],
[ 5.45911619e-04]]] 1 / Myr2>
Another useful method is
mass_enclosed(), which numerically
estimates the mass enclosed within a spherical shell defined by the specified
position. This numerically estimates \(\frac{d \Phi}{d r}\) along the vector
pointing at the specified position and estimates the enclosed mass simply as
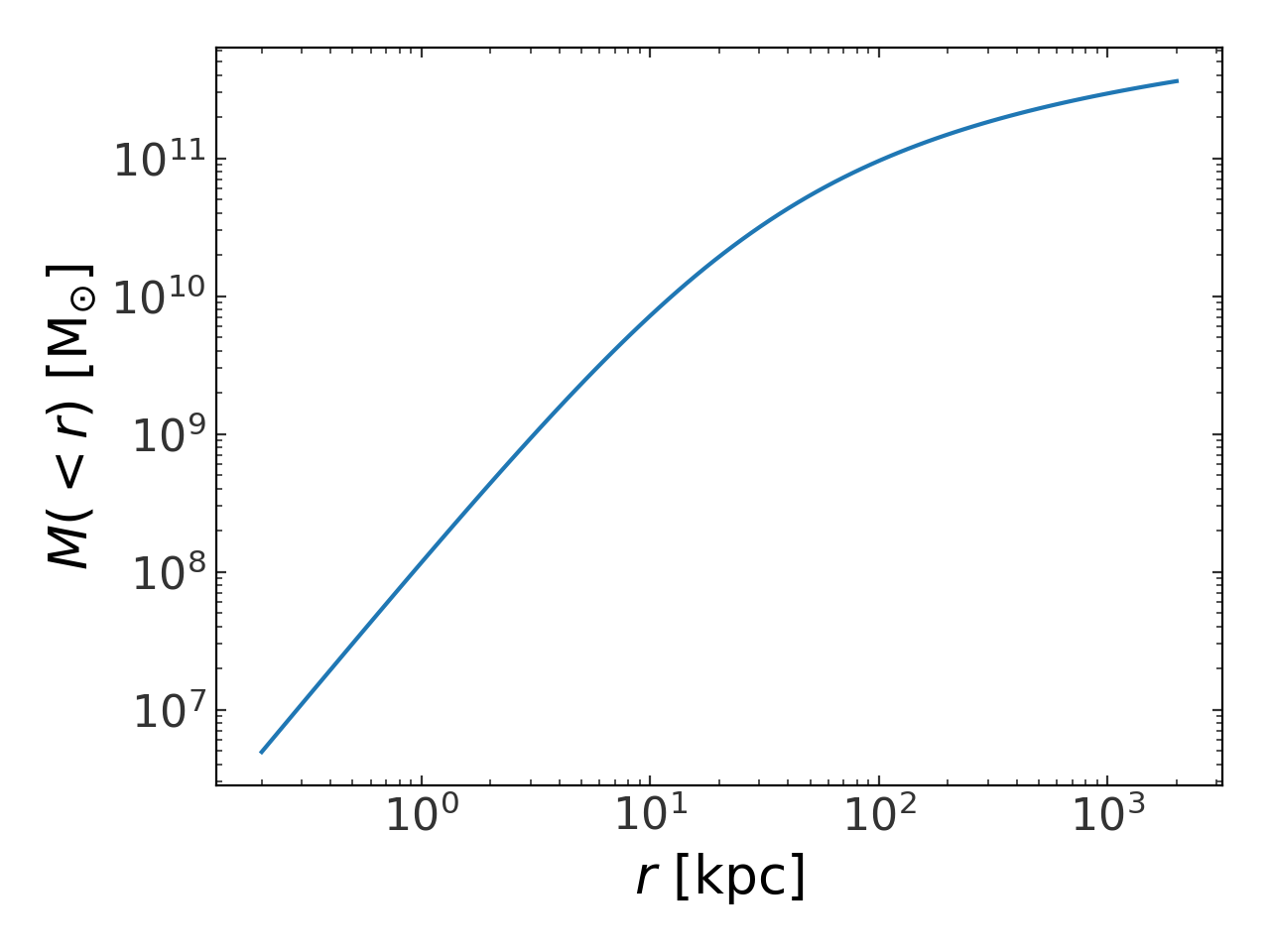
\(M(<r)\approx\frac{r^2}{G} \frac{d \Phi}{d r}\). This function can be used
to compute, for example, a mass profile:
>>> pot = gp.NFWPotential(m=1E11*u.Msun, r_s=20.*u.kpc, units=galactic)
>>> pos = np.zeros((3,100)) * u.kpc
>>> pos[0] = np.logspace(np.log10(20./100.), np.log10(20*100.), pos.shape[1]) * u.kpc
>>> m_profile = pot.mass_enclosed(pos)
>>> plt.loglog(pos[0], m_profile, marker='')
>>> plt.xlabel("$r$ [{}]".format(pos.unit.to_string(format='latex')))
>>> plt.ylabel("$M(<r)$ [{}]".format(m_profile.unit.to_string(format='latex')))
(Source code, png, pdf)
Plotting Equipotential and Isodensity contours#
Potential objects provide specialized methods for visualizing the isopotential
(plot_contours()) or isodensity
(plot_density_contours()) contours
of a given potential object. These methods plot either 1D slices or 2D contour
plots of isopotentials and isodensities. To plot a 1D slice over the dimension
of interest, pass in a grid of values for that dimension and numerical values
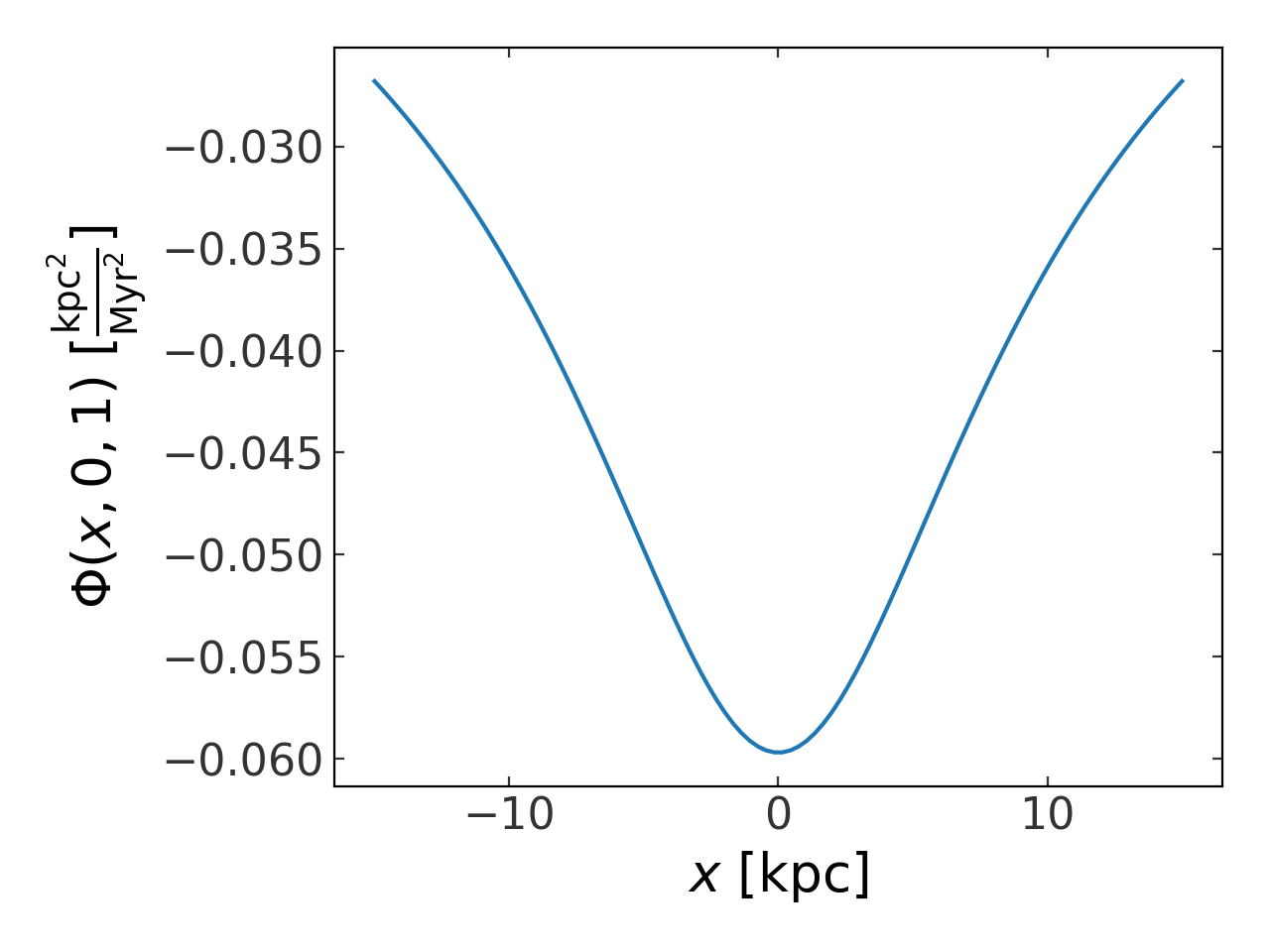
for the others. For example, to make a 1D plot of the potential value as a
function of \(x\) position at \(y=0, z=1\):
>>> p = gp.MiyamotoNagaiPotential(m=1E11, a=6.5, b=0.27, units=galactic)
>>> fig, ax = plt.subplots()
>>> p.plot_contours(grid=(np.linspace(-15,15,100), 0., 1.), marker='', ax=ax)
>>> E_unit = p.units['energy'] / p.units['mass']
>>> ax.set_xlabel("$x$ [{}]".format(p.units['length'].to_string(format='latex')))
>>> ax.set_ylabel("$\Phi(x,0,1)$ [{}]".format(E_unit.to_string(format='latex')))
(Source code, png, pdf)
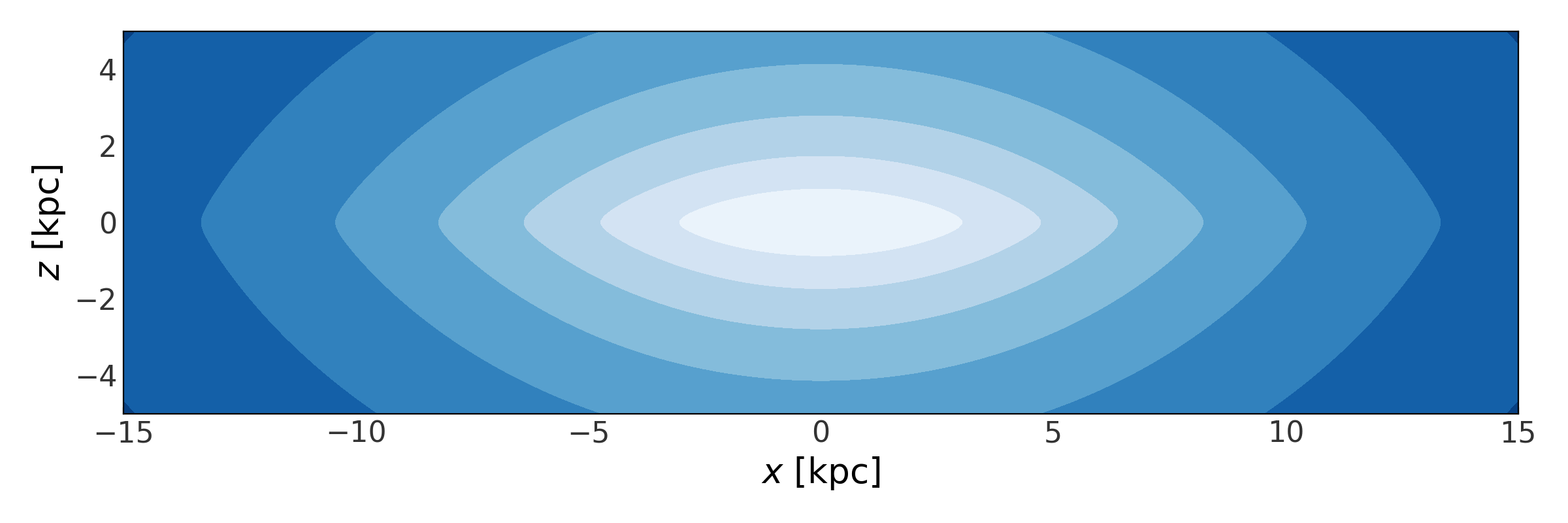
To instead make a 2D contour plot over \(x\) and \(z\) along with
\(y=0\), pass in a 1D grid of values for \(x\) and a 1D grid of values
for \(z\) (the meshgridding is taken care of internally). Here, we choose
to draw on a pre-defined matplotlib axes object so we can set the labels and
aspect ratio of the plot:
>>> fig,ax = plt.subplots(1, 1, figsize=(12, 4))
>>> x = np.linspace(-15, 15, 100)
>>> z = np.linspace(-5, 5, 100)
>>> p.plot_contours(grid=(x, 1., z), ax=ax)
>>> ax.set_xlabel("$x$ [kpc]")
>>> ax.set_ylabel("$z$ [kpc]")
(Source code, png, pdf)
Saving / loading potential objects#
Potential objects can be pickled
and can therefore be stored for later use. However, pickles are saved as binary
files. It may be useful to save to or load from text-based specifications of
Potential objects. This can be done with the
save() method and the
load() function, which serialize and
de-serialize (respectively) a Potential object to a YAML file:
>>> from gala.potential import load
>>> pot = gp.NFWPotential(m=6E11*u.Msun, r_s=20.*u.kpc,
... units=galactic)
>>> pot.save("potential.yml")
>>> load("potential.yml")
<NFWPotential: m=6.00e+11, r_s=20.00, a=1.00, b=1.00, c=1.00 (kpc,Myr,solMass,rad)>
Exporting potentials as sympy expressions#
Most of the potential classes can be exported to a sympy expression that can
be used to manipulate or evaluate the form of the potential. To access this
functionality, the potential classes have a
to_sympy classmethod (note: this
requires sympy to be installed):
>>> expr, vars_, pars = gp.LogarithmicPotential.to_sympy()
>>> str(expr)
'0.5*v_c**2*log(r_h**2 + z**2/q3**2 + y**2/q2**2 + x**2/q1**2)'
This method also returns a dictionary containing the coordinate variables used
in the expression as sympy symbols, here defined as vars_:
>>> vars_
{'x': x, 'y': y, 'z': z}
A second dictionary containing the potential parameters as sympy symbols is
also returned, here defined as pars:
>>> pars
{'v_c': v_c, 'r_h': r_h, 'q1': q1, 'q2': q2, 'q3': q3, 'phi': phi, 'G': G}
The expressions and variables returned can be used to perform operations on the
potential expression. For example, to create a sympy expression for the
gradient of the potential:
>>> import sympy as sy
>>> grad = sy.derive_by_array(expr, list(vars_.values()))
>>> grad[0] # dPhi/dx
1.0*v_c**2*x/(q1**2*(r_h**2 + z**2/q3**2 + y**2/q2**2 + x**2/q1**2))
Using gala.potential#
More details are provided in the linked pages below:
API#
gala.potential.potential Package#
Functions#
|
Create a potential class from an expression for the potential. |
|
Read a potential specification file and return a |
|
Write a |
Classes#
|
An implementation of the |
|
The Burkert potential that well-matches the rotation curve of dwarf galaxies. |
|
|
|
A baseclass for defining gravitational potentials implemented in C. |
|
A potential composed of several distinct components. |
|
A flexible potential model that uses spline interpolation over a 2D grid in cylindrical R-z coordinates. |
|
Represents an N-dimensional harmonic oscillator. |
|
The Hénon-Heiles potential. |
|
Hernquist potential for a spheroid. |
|
The Isochrone potential. |
|
Jaffe potential for a spheroid. |
|
The Kepler potential for a point mass. |
|
Kuzmin potential for a flattened mass distribution. |
|
The Galactic potential used by Law and Majewski (2010) to represent the Milky Way as a three-component sum of disk, bulge, and halo. |
|
Approximation of a Triaxial NFW Potential with the flattening in the density, not the potential. |
|
Triaxial logarithmic potential. |
|
A simple, triaxial model for a galaxy bar. |
|
A sum of three Miyamoto-Nagai disk potentials that approximate the potential generated by a double exponential disk. |
|
A simple mass-model for the Milky Way consisting of a spherical nucleus and bulge, a Miyamoto-Nagai disk, and a spherical NFW dark matter halo. |
|
A mass-model for the Milky Way consisting of a spherical nucleus and bulge, a 3-component sum of Miyamoto-Nagai disks to represent an exponential disk, and a spherical NFW dark matter halo. |
|
Miyamoto-Nagai potential for a flattened mass distribution. |
|
A perturbing potential represented by a multipole expansion. |
|
General Navarro-Frenk-White potential. |
|
A null potential with 0 mass. |
|
Plummer potential for a spheroid. |
|
A baseclass for defining pure-Python gravitational potentials. |
|
A spherical power-law density profile with an exponential cutoff. |
|
Satoh potential for a flattened mass distribution. |
|
Stone potential from Stone & Ostriker (2015). |
Class Inheritance Diagram#
digraph inheritanced63486ecac { bgcolor=transparent; rankdir=LR; size="8.0, 12.0"; "BovyMWPotential2014" [URL="../api/gala.potential.potential.BovyMWPotential2014.html#gala.potential.potential.BovyMWPotential2014",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="An implementation of the ``MWPotential2014``"]; "CCompositePotential" -> "BovyMWPotential2014" [arrowsize=0.5,style="setlinewidth(0.5)"]; "BurkertPotential" [URL="../api/gala.potential.potential.BurkertPotential.html#gala.potential.potential.BurkertPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="The Burkert potential that well-matches the rotation curve of dwarf galaxies."]; "CPotentialBase" -> "BurkertPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "CCompositePotential" [URL="../api/gala.potential.potential.CCompositePotential.html#gala.potential.potential.CCompositePotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top"]; "CompositePotential" -> "CCompositePotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "CPotentialBase" -> "CCompositePotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "CPotentialBase" [URL="../api/gala.potential.potential.CPotentialBase.html#gala.potential.potential.CPotentialBase",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="A baseclass for defining gravitational potentials implemented in C."]; "PotentialBase" -> "CPotentialBase" [arrowsize=0.5,style="setlinewidth(0.5)"]; "CommonBase" [fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled"]; "CompositePotential" [URL="../api/gala.potential.potential.CompositePotential.html#gala.potential.potential.CompositePotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="A potential composed of several distinct components. For example,"]; "PotentialBase" -> "CompositePotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "OrderedDict" -> "CompositePotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "CylSplinePotential" [URL="../api/gala.potential.potential.CylSplinePotential.html#gala.potential.potential.CylSplinePotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="A flexible potential model that uses spline interpolation over a 2D grid in"]; "CPotentialBase" -> "CylSplinePotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "HarmonicOscillatorPotential" [URL="../api/gala.potential.potential.HarmonicOscillatorPotential.html#gala.potential.potential.HarmonicOscillatorPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="Represents an N-dimensional harmonic oscillator."]; "PotentialBase" -> "HarmonicOscillatorPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "HenonHeilesPotential" [URL="../api/gala.potential.potential.HenonHeilesPotential.html#gala.potential.potential.HenonHeilesPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="The Hénon-Heiles potential."]; "CPotentialBase" -> "HenonHeilesPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "HernquistPotential" [URL="../api/gala.potential.potential.HernquistPotential.html#gala.potential.potential.HernquistPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="Hernquist potential for a spheroid."]; "CPotentialBase" -> "HernquistPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "IsochronePotential" [URL="../api/gala.potential.potential.IsochronePotential.html#gala.potential.potential.IsochronePotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="The Isochrone potential."]; "CPotentialBase" -> "IsochronePotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "JaffePotential" [URL="../api/gala.potential.potential.JaffePotential.html#gala.potential.potential.JaffePotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="Jaffe potential for a spheroid."]; "CPotentialBase" -> "JaffePotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "KeplerPotential" [URL="../api/gala.potential.potential.KeplerPotential.html#gala.potential.potential.KeplerPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="The Kepler potential for a point mass."]; "CPotentialBase" -> "KeplerPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "KuzminPotential" [URL="../api/gala.potential.potential.KuzminPotential.html#gala.potential.potential.KuzminPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="KuzminPotential(m, a, units=None, origin=None, R=None)"]; "CPotentialBase" -> "KuzminPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "LM10Potential" [URL="../api/gala.potential.potential.LM10Potential.html#gala.potential.potential.LM10Potential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="The Galactic potential used by Law and Majewski (2010) to represent"]; "CCompositePotential" -> "LM10Potential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "LeeSutoTriaxialNFWPotential" [URL="../api/gala.potential.potential.LeeSutoTriaxialNFWPotential.html#gala.potential.potential.LeeSutoTriaxialNFWPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="LeeSutoTriaxialNFWPotential(v_c, r_s, a, b, c, units=None, origin=None, R=None)"]; "CPotentialBase" -> "LeeSutoTriaxialNFWPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "LogarithmicPotential" [URL="../api/gala.potential.potential.LogarithmicPotential.html#gala.potential.potential.LogarithmicPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="LogarithmicPotential(v_c, r_h, q1, q2, q3, phi=0, theta=0, psi=0, units=None,"]; "CPotentialBase" -> "LogarithmicPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "LongMuraliBarPotential" [URL="../api/gala.potential.potential.LongMuraliBarPotential.html#gala.potential.potential.LongMuraliBarPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="LongMuraliBarPotential(m, a, b, c, alpha=0, units=None, origin=None, R=None)"]; "CPotentialBase" -> "LongMuraliBarPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "MN3ExponentialDiskPotential" [URL="../api/gala.potential.potential.MN3ExponentialDiskPotential.html#gala.potential.potential.MN3ExponentialDiskPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="MN3ExponentialDiskPotential(m, h_R, h_z, positive_density=True, sech2_z=True,"]; "CPotentialBase" -> "MN3ExponentialDiskPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "MilkyWayPotential" [URL="../api/gala.potential.potential.MilkyWayPotential.html#gala.potential.potential.MilkyWayPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="A simple mass-model for the Milky Way consisting of a spherical nucleus and"]; "CCompositePotential" -> "MilkyWayPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "MilkyWayPotential2022" [URL="../api/gala.potential.potential.MilkyWayPotential2022.html#gala.potential.potential.MilkyWayPotential2022",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="A mass-model for the Milky Way consisting of a spherical nucleus and bulge, a"]; "CCompositePotential" -> "MilkyWayPotential2022" [arrowsize=0.5,style="setlinewidth(0.5)"]; "MiyamotoNagaiPotential" [URL="../api/gala.potential.potential.MiyamotoNagaiPotential.html#gala.potential.potential.MiyamotoNagaiPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="MiyamotoNagaiPotential(m, a, b, units=None, origin=None, R=None)"]; "CPotentialBase" -> "MiyamotoNagaiPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "MultipolePotential" [URL="../api/gala.potential.potential.MultipolePotential.html#gala.potential.potential.MultipolePotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="A perturbing potential represented by a multipole expansion."]; "CPotentialBase" -> "MultipolePotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "NFWPotential" [URL="../api/gala.potential.potential.NFWPotential.html#gala.potential.potential.NFWPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="NFWPotential(m, r_s, a=1, b=1, c=1, units=None, origin=None, R=None)"]; "CPotentialBase" -> "NFWPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "NullPotential" [URL="../api/gala.potential.potential.NullPotential.html#gala.potential.potential.NullPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="NullPotential(units=None, origin=None, R=None)"]; "CPotentialBase" -> "NullPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "OrderedDict" [URL="https://docs.python.org/3/library/collections.html#collections.OrderedDict",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="Dictionary that remembers insertion order"]; "PlummerPotential" [URL="../api/gala.potential.potential.PlummerPotential.html#gala.potential.potential.PlummerPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="Plummer potential for a spheroid."]; "CPotentialBase" -> "PlummerPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "PotentialBase" [URL="../api/gala.potential.potential.PotentialBase.html#gala.potential.potential.PotentialBase",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="A baseclass for defining pure-Python gravitational potentials."]; "CommonBase" -> "PotentialBase" [arrowsize=0.5,style="setlinewidth(0.5)"]; "PowerLawCutoffPotential" [URL="../api/gala.potential.potential.PowerLawCutoffPotential.html#gala.potential.potential.PowerLawCutoffPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="A spherical power-law density profile with an exponential cutoff."]; "CPotentialBase" -> "PowerLawCutoffPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "SatohPotential" [URL="../api/gala.potential.potential.SatohPotential.html#gala.potential.potential.SatohPotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="SatohPotential(m, a, b, units=None, origin=None, R=None)"]; "CPotentialBase" -> "SatohPotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; "StonePotential" [URL="../api/gala.potential.potential.StonePotential.html#gala.potential.potential.StonePotential",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="StonePotential(m, r_c, r_h, units=None, origin=None, R=None)"]; "CPotentialBase" -> "StonePotential" [arrowsize=0.5,style="setlinewidth(0.5)"]; }gala.potential.frame.builtin Package#
Classes#
|
Represents a constantly rotating reference frame. |
|
Represents a static intertial reference frame. |
Class Inheritance Diagram#
digraph inheritancee0f9211d63 { bgcolor=transparent; rankdir=LR; size="8.0, 12.0"; "CFrameBase" [fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled"]; "FrameBase" -> "CFrameBase" [arrowsize=0.5,style="setlinewidth(0.5)"]; "CommonBase" [fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled"]; "ConstantRotatingFrame" [URL="../api/gala.potential.frame.builtin.ConstantRotatingFrame.html#gala.potential.frame.builtin.ConstantRotatingFrame",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="Represents a constantly rotating reference frame."]; "CFrameBase" -> "ConstantRotatingFrame" [arrowsize=0.5,style="setlinewidth(0.5)"]; "FrameBase" [fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled"]; "CommonBase" -> "FrameBase" [arrowsize=0.5,style="setlinewidth(0.5)"]; "StaticFrame" [URL="../api/gala.potential.frame.builtin.StaticFrame.html#gala.potential.frame.builtin.StaticFrame",fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=10,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="Represents a static intertial reference frame."]; "CFrameBase" -> "StaticFrame" [arrowsize=0.5,style="setlinewidth(0.5)"]; }gala.potential.hamiltonian Package#
Classes#
|
Represents a composition of a gravitational potential and a reference frame. |
