Generating mock stellar streams#
Introduction#
This module contains functions for generating mock stellar streams using a variety of methods that approximate the formation of streams in N-body simulations. Mock streams are generated by specifying time-stepping and release time information (i.e., when should stream particles be generated), and by specifying the stream distribution function (DF) to use to generate initial conditions for the stream particles. The former is customizable, and a number of popular stream DFs are implemented.
Some imports needed for the code below:
>>> import astropy.units as u
>>> import numpy as np
>>> import gala.potential as gp
>>> import gala.dynamics as gd
>>> from gala.dynamics import mockstream as ms
>>> from gala.units import galactic
We will also set the default Astropy Galactocentric frame parameters to the values adopted in Astropy v4.0:
>>> import astropy.coordinates as coord
>>> _ = coord.galactocentric_frame_defaults.set('v4.0')
Getting started#
All mock stream generation done using the built-in gravitational potential
models implemented in gala.potential, so we must first specify a gravitational
potential to integrate orbits in. For the examples below, we will use a
spherical NFW potential with a circular velocity at the scale radius of 220
km/s, and a scale radius of 15 kpc:
>>> pot = gp.NFWPotential.from_circular_velocity(v_c=220*u.km/u.s,
... r_s=15*u.kpc,
... units=galactic)
The mock stream generation supports any of the reference frames implemented in
gala (e.g., non-static / rotating reference frames), so we must create a
Hamiltonian object to use when generating streams.
By default, this will use a static reference frame:
>>> H = gp.Hamiltonian(pot)
Next, we will create initial conditions for the progenitor system. In this case, we will generate the mock stream starting from this position going forward in time. However, this is customizable: if you instead have the final position of the progenitor system, there is a convenient way of doing this described below (see Generating a stream from the present-day progenitor location). Let’s specify a position and velocity that we think will produce a mildly eccentric orbit in the x-y plane of our coordinate system:
>>> prog_w0 = gd.PhaseSpacePosition(pos=[10, 0, 0.] * u.kpc,
... vel=[0, 170, 0.] * u.km/u.s)
We now have to specify the method for generating stream particles, i.e., the
stream distribution function (DF). For this example, we will use the method
implemented in [fardal15], incuded in gala as
FardalStreamDF. Other methods of note are
StreaklineStreamDF from [kuepper12], and
LagrangeCloudStreamDF based on [gibbons14]. Each of
the StreamDF classes take a few common arguments, such as lead and
trail, which are boolean arguments that control whether to generate both
leading and trailing tails, or just one or the other. By default, both are set
to True (i.e., both leading and trailing tails are generated by default). Some
other StreamDF classes may require other parameters. Let’s create a
FardalStreamDF instance and accept the default
argument values. We will also need to specify the progenitor mass, which is
passed in to any StreamDF and is used to scale the particle release
distribution:
>>> df = ms.FardalStreamDF(gala_modified=True)
>>> prog_mass = 2.5E4 * u.Msun
Warning
The parameter values of the FardalStreamDF have been updated (fixed) in v1.9 to
match the parameter values in the final published version of [fardal15]. For now,
this class uses the Gala modified parameter values that have been adopted over the
last several years in Gala. In the future, the default behavior of this class will
use the [fardal15] parameter values instead, breaking backwards compatibility for
mock stream simulations. To use the [fardal15] parameters now, set
gala_modified=False. To continue to use the Gala modified parameter values, set
gala_modified=True.
The final step before actually generating the stream is to create a
MockStreamGenerator instance, which we will use to
actually generate the stream. This takes the StreamDF and the external
potential (Hamiltonian) as arguments:
>>> gen = ms.MockStreamGenerator(df, H)
We are now ready to run the generator and create a mock stream. To do this, we use the run() method. This accepts the progenitor orbit initial conditions (we defined above as prog_w0), the progenitor mass (we defined as prog_mass), and time-stepping information. We will integrate the progenitor orbit for 1000 steps with a timestep of 1 Myr:
>>> stream, prog = gen.run(prog_w0, prog_mass,
... dt=1 * u.Myr, n_steps=1000)
Let’s plot the stream:
>>> stream.plot(['x', 'y'])
(Source code, png, pdf)
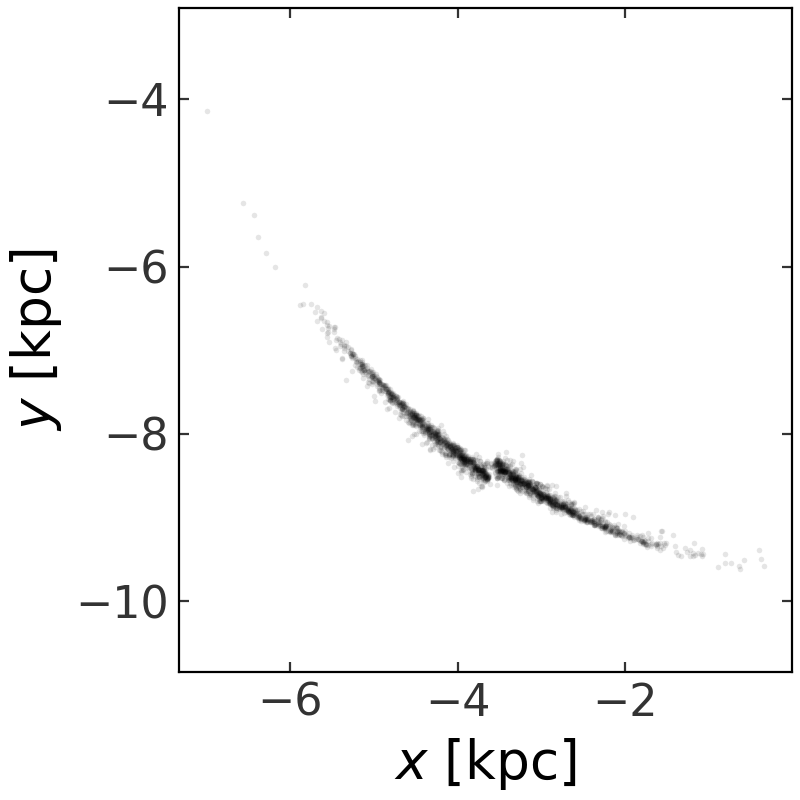
By default, two stream particles are generated at every timestep in the
integration of the progenitor orbit (specified above by the timestep dt and
number of steps n_steps). We can control the frequency of releasing
particles, and the number of particles released using the release_every and
n_particles arguments. For example, setting release_every=8 and
n_particles=2 will instead release 4 particles (2 for each tail) every 8th
timestep.
Self-gravity of the progenitor#
Also by default, the progenitor system is assumed to be massless, and the stream
particles are treated as test particles in the specified external potential or
Hamiltonian. It is possible to include a potential object for the progenitor
system to account for the self-gravity of the progenitor as stream star
particles are released. We can use any of the gala.potential potential
objects to represent the progenitor system, but here we will use a simple
PlummerPotential. We pass this in to the
MockStreamGenerator - let’s see what the stream
looks like when generated including self-gravity:
>>> prog_pot = gp.PlummerPotential(m=prog_mass, b=4*u.pc, units=galactic)
>>> gen2 = ms.MockStreamGenerator(df, H, progenitor_potential=prog_pot)
>>> stream2, prog = gen2.run(prog_w0, prog_mass,
... dt=1 * u.Myr, n_steps=1000)
>>> stream2.plot(['x', 'y'])
(Source code, png, pdf)
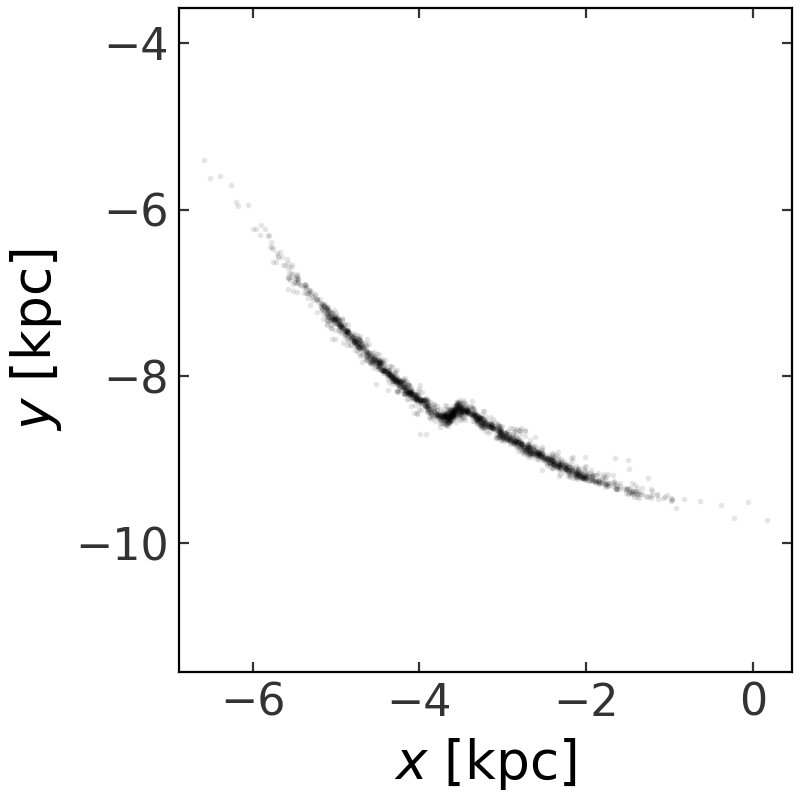
Generating a stream from the present-day progenitor location#
In the examples above, we pass in initial conditions for the progenitor and
generate the mock stream going forward in time. However, we often may want to
generate a stream such that the final progenitor location ends up at some
specified phase-space position. By convention, when a negative timestep is
passed in to run(), this is
interpreted to mean that the input progenitor phase-space position should be the
final position. Internally, this position is integrated backwards to the
earliest time, then a stream is generated forward from the past time. This is particularly useful when trying to reproduce observed streams, such as the Pal 5 stream:
>>> import astropy.coordinates as coord
>>> pal5_c = coord.SkyCoord(ra=229.018*u.degree, dec=-0.124*u.degree,
... distance=22.9*u.kpc,
... pm_ra_cosdec=-2.296*u.mas/u.yr,
... pm_dec=-2.257*u.mas/u.yr,
... radial_velocity=-58.7*u.km/u.s)
>>> rep = pal5_c.transform_to(coord.Galactocentric).data
>>> pal5_w0 = gd.PhaseSpacePosition(rep)
>>> pal5_mass = 2.5e4 * u.Msun
>>> pal5_pot = gp.PlummerPotential(m=pal5_mass, b=4*u.pc, units=galactic)
>>> mw = gp.MilkyWayPotential()
>>> gen_pal5 = ms.MockStreamGenerator(df, mw, progenitor_potential=pal5_pot)
>>> pal5_stream, _ = gen_pal5.run(pal5_w0, pal5_mass,
... dt=-1 * u.Myr, n_steps=4000)
>>> pal5_stream_c = pal5_stream.to_coord_frame(coord.ICRS)
References#
API#
Functions#
|
|
Classes#
|
A base class for representing distribution functions for generating stellar streams. |
|
A class for representing the Fardal+2015 distribution function for generating stellar streams based on Fardal et al. 2015 https://ui.adsabs.harvard.edu/abs/2015MNRAS.452..301F/abstract. |
|
A class for representing the Lagrange Cloud Stripping distribution function for generating stellar streams. |
|
Represents phase-space positions, i.e. positions and conjugate momenta (velocities). |
|
Generate a mock stellar stream in the specified external potential. |
A class for representing the "streakline" distribution function for generating stellar streams based on Kuepper et al. 2012 https://ui.adsabs.harvard.edu/abs/2012MNRAS.420.2700K/abstract. |
