Dynamics (gala.dynamics)

For the examples below the following imports have already been executed:

>>> import astropy.units as u
>>> import numpy as np
>>> import gala.potential as gp
>>> import gala.dynamics as gd
>>> from gala.units import galactic

Introduction

This subpackage contains functions and classes useful for gravitational dynamics. There are utilities for transforming orbits in phase-space to action-angle coordinates, tools for visualizing and computing dynamical quantities from orbits, tools to generate mock stellar streams, and tools useful for nonlinear dynamics such as Lyapunov exponent estimation.

The fundamental objects used by many of the functions and utilities in this and other subpackages are the PhaseSpacePosition and Orbit classes.

Getting started: Working with orbits

As a demonstration of how to use these objects, we’ll start by integrating an orbit using the gala.potential and gala.integrate subpackages:

>>> pot = gp.MiyamotoNagaiPotential(m=2.5E11*u.Msun, a=6.5*u.kpc,
...                                 b=0.26*u.kpc, units=galactic)
>>> w0 = gd.PhaseSpacePosition(pos=[11., 0., 0.2]*u.kpc,
...                            vel=[0., 200, 100]*u.km/u.s)
>>> orbit = gp.Hamiltonian(pot).integrate_orbit(w0, dt=1., n_steps=1000)

This numerically integrates an orbit from the specified initial conditions, w0, and returns an Orbit object. By default, the position and velocity are assumed to be Cartesian coordinates but other coordinate systems are supported (see the Orbit and phase-space position objects in more detail and N-dimensional representation classes pages for more information).

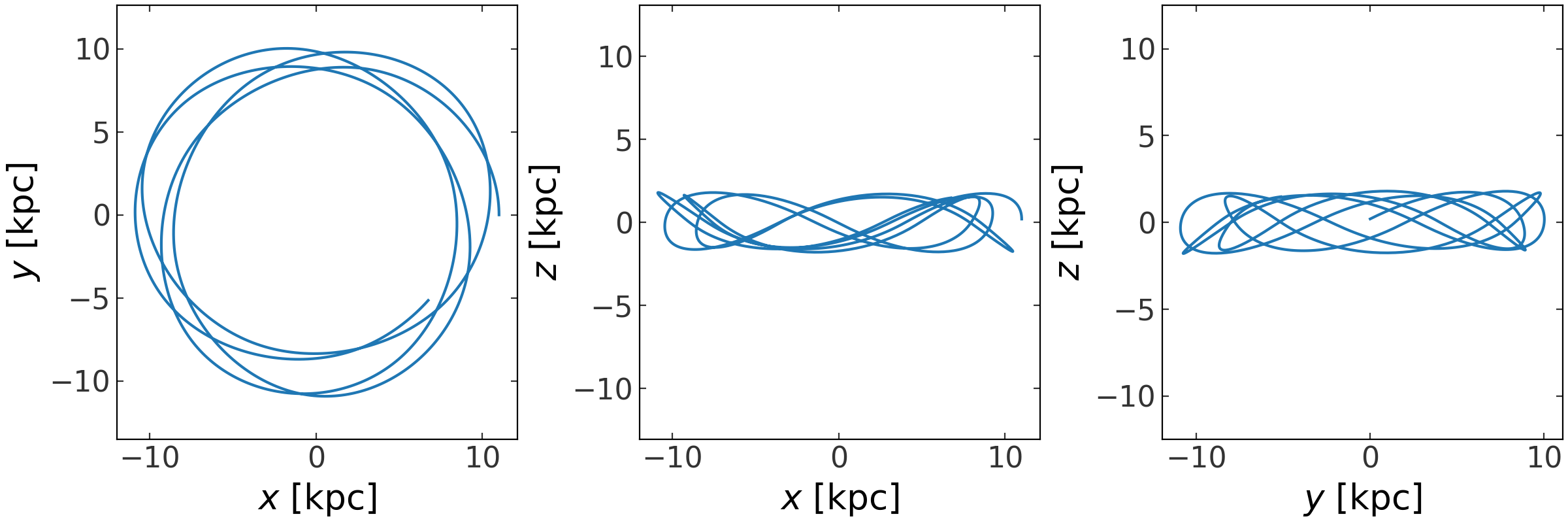
The Orbit object that is returned contains many useful methods, and can be passed to many of the analysis functions implemented in Gala. For example, we can easily visualize the orbit by plotting the time series in all Cartesian projections using the plot() method:

>>> fig = orbit.plot()

(Source code, png, pdf)

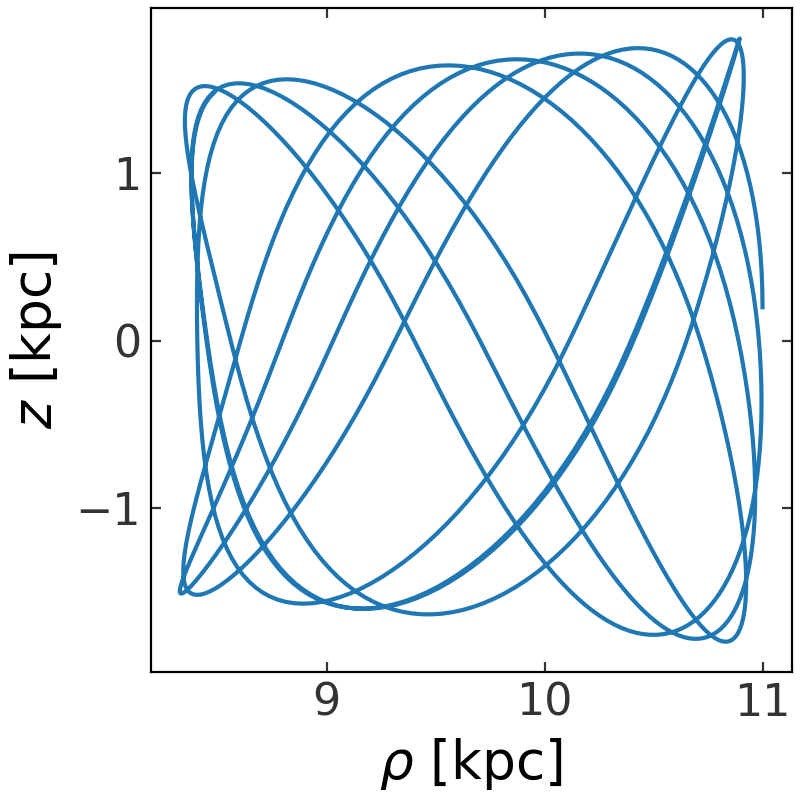
Or, we can visualize the orbit in just one projection of some transformed coordinate representation, for example, cylindrical radius \(\rho\) and \(z\):

>>> fig = orbit.represent_as('cylindrical').plot(['rho', 'z'])

(Source code, png, pdf)

From the Orbit object, we can also easily compute dynamical quantities such as the energy or angular momentum (we take the 0th element because these functions return the quantities computed at every timestep):

>>> E = orbit.energy()
>>> E[0] 
<Quantity −0.060740198 kpc2 / Myr2>

Let’s see how well the integrator conserves energy and the z component of angular momentum:

>>> Lz = orbit.angular_momentum()[2]
>>> np.std(E), np.std(Lz) 
(<Quantity 4.654233175716351e-06 kpc2 / Myr2>,
 <Quantity 9.675900603446092e-16 kpc2 / Myr>)

We can access the position and velocity components of the orbit separately using attributes that map to the underlying BaseRepresentation and BaseDifferential subclass instances that store the position and velocity data. The attribute names depend on the representation. For example, for a Cartesian representation, the position components are ['x', 'y', 'z'] and the velocity components are ['v_x', 'v_y', 'v_z']. With a Orbit or PhaseSpacePosition instance, you can check the valid compnent names using the attributes .pos_components and .vel_components:

>>> orbit.pos_components.keys() 
odict_keys(['x', 'y', 'z'])
>>> orbit.vel_components.keys() 
odict_keys(['v_x', 'v_y', 'v_z'])

Meaning, we can access these components by doing, e.g.:

>>> orbit.v_x 
<Quantity [ 0.        ,-0.00567589,-0.01129934,...,  0.18751756,
            0.18286687, 0.17812762] kpc / Myr>

For a Cylindrical representation, these are instead:

>>> cyl_orbit = orbit.represent_as('cylindrical')
>>> cyl_orbit.pos_components.keys() 
odict_keys(['rho', 'phi', 'z'])
>>> cyl_orbit.vel_components.keys() 
odict_keys(['v_rho', 'pm_phi', 'v_z'])
>>> cyl_orbit.v_rho 
<Quantity [ 0.        ,-0.00187214,-0.00369183,...,  0.01699321,
            0.01930216, 0.02159477] kpc / Myr>

Continue to the Orbit and phase-space position objects in more detail page for more information.

Using gala.dynamics

More details are provided in the linked pages below:

• Orbit and phase-space position objects in more detail
  • Introduction
  • Phase-space Positions
  • Orbits
  • More information
• N-dimensional representation classes
  • Introduction
• Transforming to actions, angles, and frequencies
  • Introduction
  • The O2GF action solver
  • Using the Staeckel Fudge in Galpy
  • References
• Generating mock stellar streams
  • Introduction
  • Getting started
  • Self-gravity of the progenitor
  • Generating a stream from the present-day progenitor location
  • References
• Nonlinear Dynamics
  • Introduction
  • Computing Lyapunov exponents
• N-body (gala.dynamics.nbody)
  • Introduction
  • Getting started
  • Example: Mixed test particle and massive particle orbit integration
  • Example: N-body integration with a background potential

API

gala.dynamics Package

Classes

Orbit(pos, vel[, t, hamiltonian, potential, ...])	Represents an orbit: positions and velocities (conjugate momenta) as a function of time.
PhaseSpacePosition(pos[, vel, frame])	Represents phase-space positions, i.e. positions and conjugate momenta (velocities).